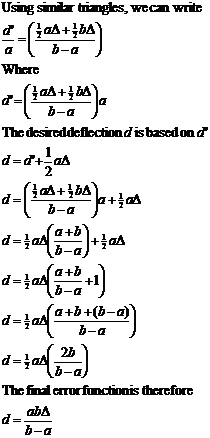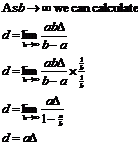3
"If you can find a path with no obstacles, it probably doesn't lead anywhere"
Frank A. Clark
Chapter 1 - Augmented reality working planes
This chapter describes new interaction techniques for augmented reality to support manipulation and construction of geometry at large distances away from the user. Existing 3D techniques previously described in Chapter 2 extend the userís interaction beyond armís reach, but focus on operating at distances relatively close to the user where there are many cues available to accurately estimate relative position. This chapter references various studies to show that beyond a certain distance the ability of humans to perceive depth is severely attenuated. This affects the accuracy of interactions that can be performed at large distances, which are important when interacting in an outside world with structures beyond the depth perception capability of humans. A new technique named AR working planes is described, using the projection of 2D cursors onto 3D planes to avoid the specification of depth values directly by the user. This technique only requires the use of 2D inputs and so can be implemented using a wide range of input devices, making it ideal for use in mobile environments. The AR working planes concept is described in detail, discussing their placement in various coordinate systems and creation relative to the user or the world. The use of AR working planes for action and construction at a distance is then described, including the manipulation of existing objects and the placement of vertices to create new geometry. To perform operations using AR working planes, it is important that the plane is correctly aligned with the physical world to ensure the accurate capture of information. I demonstrate that an accurate way to perform this is by using the eye to align physical world features and therefore ensuring the body and head are correctly placed. Using the AR working planes technique developed in this chapter, the human is capable of performing interactions that are limited only by the accuracy of the tracking equipment in use and not by their lack of depth estimation capabilities.
1.1 Distance estimation cues
|
|
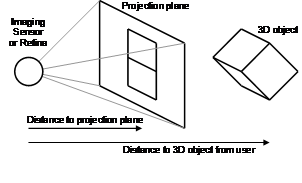
Humans gauge the distance to objects and their layout through visual cues acquired with the eyes, along with any other available senses such as sound, touch, and smell. The human sense of vision is unique in that it is capable of gathering information from a virtually infinite range of distances, whereas other senses tend to be useful only within close range. Human vision can be approximately modelled as a 2D array of pixels (similar to a video camera) gathering light to produce a 2D image representing the 3D environment. While horizontal and vertical placement of objects in the image is easily obtainable, depth is ambiguous due to the flattened representation of the image, as depicted in Figure 3‑1. Depth information can only be estimated by analysing the contents of the images captured. The eyes and brain process a number of vision cues that occur in images to determine the depth positioning of objects in the scene, and are combined together to improve accuracy. Drascic and Milgram [DRAS96] present a survey of perceptual issues in AR, discussing various depth cues and how mixed reality systems are limited in presenting them to the user. Cutting and Vishton [CUTT95] followed by Cutting [CUTT97] [CUTT02] provide detailed surveys on previous work in the area of perception and the determination of distance relationships between objects using visual cues. Cutting and Vishton collected results from a large number of previous studies and categorised nine cues (rejecting another six), describing the range they are accurate over and the kind of depth information that can be extracted. Not all visual cues can produce absolute measurement information however; some cues can only provide relative ratios between objects or simple ordering information. The nine cues described by Cutting and Vishton [CUTT95] are as follows:
∑ Occlusion Ė when objects at varying distances are projected onto the retina of the human, objects that are closer will overlap objects that are further away. This allows ordering information to be extracted and works over any distance, but cannot be used to form any absolute measurements.
Relative size Ė by measuring the size of a projected image on the retina and knowing that two objects are of a similar size, both ordering and size ratios can be calculated but without absolute values. No prior knowledge of the objectís size is required for this cue except that the objects are of the same size, and can be placed at any visible distance.
Relative density Ė this cue is similar to relative size and uses two similar objects (but of unknown sizes) and compares the density of textures that are placed on them. By comparing the texture patterns, ordering and size can be calculated, although absolute values are still not possible. This cue is also useable at any distance, assuming the objects are visible.
Height in the visual field Ė this cue relies on gauging the distance of objects by comparing their heights relative to each other. Assuming the objects are all placed onto the ground plane, that the eye is at a known height, and that the ground is indeed flat, then this cue can produce absolute distance measurements. In most cases however, not all the previous conditions can be met and so only ordering is available. This cue is only effective from about 2 metres onwards as the human must be able to see the objects touching the ground plane.
Aerial perspective Ė when objects such as mountains and buildings are at very large distances, environmental effects such as fog, lighting, and distortion begin to affect the image of objects. As distance increases, the image of objects becomes gradually more attenuated and so this can be used as a measure of distance. Since this cue is only effective at large distances, calculating absolute values based on the attenuation of objects may be difficult since they might not be easily visible.
Motion perspective Ė when moving sideways through the environment, images of objects that are at a distance will move across the retina slower than closer objects, caused by perspective distortion. This cue attenuates over distance and works best when the eye can easily focus onto the objects in motion; therefore objects that are so close that they move by very quickly will be difficult to process. While absolute distances may be extracted given knowledge of the movement and height of the eye, motion perspective is best able to be used for relative ratios and ordering.
Convergence Ė when objects are in close range, the eyes will adjust their angle to point toward the object of interest. As the distance increases, the angle of the eyes gradually widens to the point where they are both looking in parallel directions when an object is at very large distances. Convergence requires knowledge of the distance between the eyes, and when used within a range of about two metres, this cue is able to give accurate absolute distance measurements.
Accommodation Ė in order to perceive objects clearly, the eyes will focus the image by adjusting internal lenses controlled by a muscle, similar to a camera. This cue can be used to calculate distance for an object, and is usually combined together with convergence. Accommodation operates up to approximately two metres, although the eyeís ability to focus deteriorates with age. Similar to convergence, absolute distance information within its limitations can be calculated.
Binocular disparities Ė when two eyes are both focused on the same object, if it is within a close range the images presented to each eye will vary slightly. Using the eyes in stereo may capture depth information with absolute values assuming the distance between the eyes and convergence is known, and also correspondences between points in the images can be found. This cue produces absolute distances from very close ranges and attenuates linearly as distance increases.
Cutting and Vishton also mention a number of other cues discussed in various literature, but eliminate them from consideration because they are based on the previously identified cues, or not demonstrated as being effective during user studies. In normal daily life, the brain combines these cues together to produce situational awareness for the human. In VR environments, some of these cues can be simulated with the use of HMDs. HMDs can produce stereo images with offsets to match the distance between the eyes, and software can simulate fog and some environmental effects. While stereo HMDs give the user some feeling of depth perception, this is limited because the brain may be confused by inconsistencies in the sensor information normally acquired.
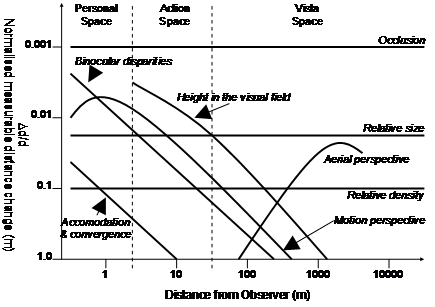
To summarise the various cues and their effectiveness at different distances, Cutting and Vishton produced a graph depicted in Figure 3‑2 that indicates the accuracy of each cue. This figure uses a log scale for distance along the X axis, and a normalised log scale along the Y axis with the smallest distance change measurable divided by distance. A value of 0.1 on the Y axis may indicate the ability to discern a 1 metre change at a distance of 10 metres, or a 10 metre change at a distance of 100 metres. Each of these curves is based on the data from numerous previously performed user studies and demonstrates that each cue is effective at different distances.
Based on their analysis of the nine available cues, Cutting and Vishton defined three separate spaces around the body at different distances to better categorise the depth estimation available. The first area defined is named personal space and ranges from the body to up to 2 metres. Personal space is where humans perform most of their close up interactions, and so depth perception is highly refined due to its importance in daily life. From 2 to 30 metres is a second area termed action space. In this space, users may interact reasonably accurately with other objects (such as throwing a ball to hit a target), but with less cues and accuracy than personal space. Beyond 30 metres is vista space, where objects appear flat and distance estimations become quite poor compared to closer spaces. Figure 3‑2 includes divisions showing where the three spaces are located relative to the accuracy curves previously described.
|
|
|
Figure 2‑2 Normalised effectiveness of various depth perception cues over distance (Adapted from Cutting and Vishton [CUTT95]) |
Based on this discussion, it seems that a humanís ability to reconstruct 3D information about a scene is most capable when operating within close range to the body. Since humans mainly deal with objects that are within armís reach, this sense (named proprioception) is highly refined and was used by Mine to improve user interfaces for 3D environments [MINE97a]. At larger distances however, these abilities attenuate very rapidly to the point where beyond 30 metres or so it is difficult to perceive absolute distances. When modelling large outdoor structures such as buildings, distances of 30 metres or greater are quite common. If distances cannot be perceived accurately for the modelling tasks required, then performing action and construction at a distance operations will require extra assistance to be useable.
1.2 AR working planes definition
|
|
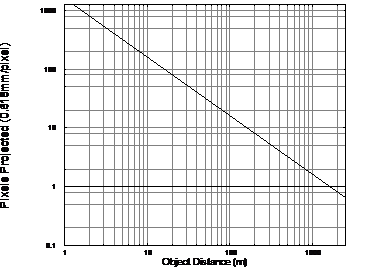
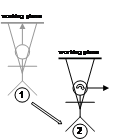
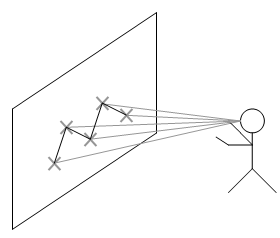
Previously described techniques such as working planes [MINE97a], selection apertures [FORS96], and image planes [PIER97] were developed to project the locations of display-based cursors onto a 3D environment. These techniques are useful for selection and manipulation operations in vista space because there are no restrictions on the range of use, and the techniques are just as easy to use within armís reach or kilometres away. Image planes and selection apertures are not capable of specifying distance however, since the plane from the view frustum is used for the cursors and depth is not required to be resolved. Assuming a typical perspective projection, the accuracy of vertical and horizontal motion in all of these techniques is proportional to the size and distance of the object, but attenuates at a constant rate less than that of human depth perception. With the use of HMDs, the cursor is represented using pixels and introduces a pyramid of uncertainty specified by the pixel size at the projection plane. To simplify this argument, I will ignore anti-aliasing effects that may occur when points and lines are drawn smoothly onto pixel arrays. Figure 3‑3 plots the effect of distance on the projection of a 1 metre object onto a Sony Glasstron PLM-700E HMD with pixels of size 0.618 mm at 1 metre from the eye (the derivation of this value is described in Section 3.8). From Figure 3‑3, it can be observed that the 1 metre object is not properly visible beyond approximately 1618 metres since it is less than a single pixel in size. An important property of interactive modelling is that users can only perform manipulations that are visually verifiable. There is no need to provide the user with the capability to move a mountain on the horizon 5 centimetres to the right because it is not visually noticeable. Only by approaching the object will the user notice any accuracy problems, and these can then be corrected since it is a change that can be verified. Based on this argument, the use of projection techniques imposes no accuracy limitations noticeable by the user.
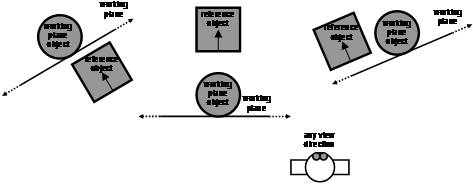
Using the previously discussed projection concepts, these can be extended into the AR domain to perform interactive modelling outdoors. I have developed a concept named augmented reality working planes that is based on the working planes concept used in traditional CAD systems. AR working planes can be created in the environment relative to the user or other objects, and stored in one of four possible coordinate systems. These planes can then be used as a surface to project a 2D cursor on to, resolving full 3D coordinates to manipulate existing objects and create new vertices. Since planes are by definition infinite in size, the user can project the cursor onto the plane from almost any location, although the accuracy decreases as the plane becomes parallel to the userís view. AR working planes improves on existing image plane-based techniques because the plane can be any arbitrary surface, allowing the calculation of depth at any distance and interaction in all three dimensions. This technique is also a mobile alternative to desktop CAD systems because the 3D view and working planes can be specified using the body in the physical world. To control the cursor projected against the AR working plane, any 2D input device can be used. The cursor is projected onto the surface of the plane and so no depth information is required, allowing a wide range of input devices to be used. Chapter 5 focuses on the implementation of a mobile input device suitable for use with AR working planes.
The use of AR working planes does impose some limitations on the user, and requires them to specify distance by creating a plane and then drawing against it from a different direction. Two operations from separate locations and orientations are usually required so that depth can be extracted without requiring the user to estimate it. While Chapter 2 reviewed previous research by Liang and Green that indicated that the decomposing of 3D tasks into 1D or 2D units was not efficient [LIAN93], in the scenario of working in vista space there is no alternative. As a support of my argument, Ware [WARE88] and Hinckley [HINC94a] both state that reducing degrees of freedom is useful when it is hard to maintain precision in certain degrees while adjusting others. In vista space, depth estimation is poor and so removing this degree of freedom is the best option to preserve accuracy.
1.3 Coordinate systems
In CAD systems, working planes can be placed in the environment using exact numeric keyboard entry, by drawing the planeís cross section from a perpendicular view, or by selecting another objectís facet [MINE97b]. The first two cases may be difficult and unintuitive because people think in terms of objects relative to their body rather than abstract coordinate systems and view points. My extensions to working planes for AR can create these planes using the userís body, making them much more intuitive to use when operating outdoors. An important improvement is that these AR working planes can be created and fixed to a number of coordinate systems that humans intuitively understand.
|
|
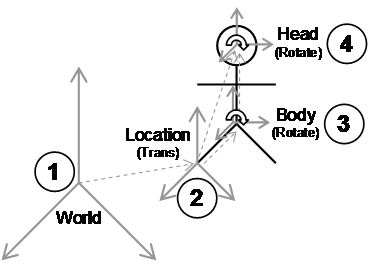
Feiner et al. discuss the presentation of information in AR displays and how this information can be in surround-fixed, display-fixed, or world-fixed coordinates [FEIN93b]. As the user moves around the virtual environment, information in each coordinate system will be displayed differently. By selecting an appropriate coordinate system for each type of information, it can be more intuitively understood by users. Mine and Brooks discuss the placement of tools such as menus and tool palettes relative to the body, and how the user can find these easily since they are carried around relative to the user [MINE97a]. Using these concepts, a number of different coordinate systems can be identified that are suitable for performing modelling tasks, as depicted in Figure 3‑4. I have named these coordinate systems world, location, body, and head. In Figure 3‑4, the user operates in a world coordinate system that is anchored to some fixed point in the physical world. Using a positioning device, location coordinates are measured relative to world coordinates and represent the location of the userís feet but without direction. Using an orientation sensor mounted on the hips, body-relative coordinates can be calculated by applying an offset to transform from the feet to the hips and then applying the orientation. Head-relative coordinates are similarly calculated with the appropriate height and orientation of the userís head. The height values used for body and head coordinates can be either measured once and stored as a constant, or captured from a tracking device. I have only identified these coordinate systems as the main ones of importance for this research, but there are many others if appropriate tracking devices are available.
Information can be stored relative to any of the coordinate systems described in Figure 3‑4. The surround-fixed windows by Feiner et al. map to body-relative, display-fixed windows map to head-relative, and world-fixed windows map to world-relative. The menus and tool palettes floating about the user implemented by Mine and Brooks map to body-relative. Using the coordinate systems defined here, I extend the concepts of Feiner et al. to include not only the presentation of information, but also the placement of AR working planes so that points may be created and objects manipulated at a distance. This section describes AR working planes that have been created relative to each of the four coordinate systems and the effect that user motion has on the created planes. Although body-relative coordinates are described here, they are not implemented in later chapters since no sensor is used to measure body rotation, and is included only for comparisons to existing work. Based on the orientation and position sensors that I have used, figures are used to show the effect on each AR working plane of body translation, head rotation, or combination movements in the environment.
1.3.1 World-relative coordinates
|
Translate |
Head Rotate |
Translate / Head Rotate |
|
|
|
|
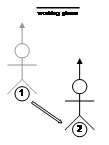
World coordinates are the top-level coordinate system used to represent positions over a planet or other large areas of interest. Objects that are specified relative to the origin of the world coordinate system are anchored to a fixed place in the physical world, and are completely independent of the userís motion, as depicted by (1) in Figure 3‑4. In virtual environments, most objects are created world-relative since they are not attached to the user and may move independently, with examples being buildings, trees, and automobiles. The userís coordinate systems are also specified in world coordinates, since their position and orientation are returned from tracking devices that are world-relative. Figure 3‑5 depicts a user moving in the environment with the AR working plane remaining since it is in coordinates independent of the user. World-relative AR working planes are commonly used when working with buildings and the user desires to keep the planes fixed relative to the walls at all times.
|
Translate |
Head Rotate |
Translate / Head Rotate |
|
|
|
|
1.3.2 Location-relative coordinates
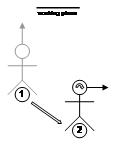
Location coordinates are derived by taking the current position of the user from a tracking device and adding this to the origin of the world coordinate system. The axes for both location and world coordinates are still aligned except there is a translation offset between the two, as depicted by (2) in Figure 3‑4. With location coordinates the orientation of the user has not been applied, and so any changes in rotation will have no effect. An object placed in location-relative coordinates will always appear at the same true compass bearing from the user and maintain the same distance during motion. Location-relative coordinates are particularly useful for displaying an immersive compass to the user - the compass labels are attached around the user at a fixed radius and stay at the same orientation no matter what direction the user is looking. Another use is to attach a virtual camera at a fixed distance and direction from the user at all times, which follows the userís location but does not move with head or body rotation. Figure 3‑6 depicts the effects of user motion on an AR working plane that is location-relative, where the plane moves with the user around the world. With user translation the plane moves with the same transformation, but rotation has no effect. The main uses for location-relative coordinate systems are the placement of vertices and object manipulation at fixed orientations. These fixed orientations are useful when working with buildings, keeping the AR working plane parallel to the walls but still moving relative to the user.
1.3.3 Body-relative coordinates
|
Translate |
Head Rotate |
Translate / Head Rotate |
|
|
|
|
|
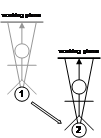
Figure 2‑7 Body-relative AR working planes remain at a fixed orientation and distance to the hips and are not modified by motion of the head |
Although it is possible to define any number of coordinate systems, this will not be performed since in many cases it does not make sense to create objects relative to arbitrary parts of the body. A userís sense of proprioception is focused about its main components such as the hips and the head, and so these will be the main focus. Body coordinates are defined relative to location coordinates except that orientation of the hips is added, as depicted by (3) in Figure 3‑4. Objects placed in body-relative coordinates will always appear in the same location-relative to the hips as the user moves around, with a good example being a tool belt worn by a worker. When walking around or when moving the head, the tool belt always remains in the same fixed position, ready to be accessed by the hands. Body-relative differs from location-relative in that the rotation of the hips affects the attached objects, whereas location-relative ignores any rotations by the user. The cockpit of an aircraft is also similar, where controls are always at the same location-relative to the userís hips but the aircraft can fly around and keep the controls mapped to the same locations. Figure 3‑7 depicts the effects of user motion of the body on an AR working plane that is body-relative, where the plane is attached to the hips of the user as they move around the world. Although body coordinates are very intuitive within armís reach due to proprioception, they become more confusing at further distances since extra visual inspection is usually required. Some possible uses for body-relative coordinate systems are the placement of tools on a belt for easy access and display of non-critical status information.
1.3.4 Head-relative coordinates
Head-relative coordinates are similar to body-relative in that they add rotations to the location-relative coordinates, and can be defined relative to either location or body coordinates, as depicted by (4) in Figure 3‑4. The only difference between head-relative and body-relative coordinates is the part of the body that the information is attached to. Objects placed in head coordinates will always appear in the same location-relative to the userís head, with a good example being a floating status indicator on a HMD. No matter what the position or orientation of the user, the status indicator will always be visible at the same location. Figure 3‑8 depicts the effects of user motion of the head on an AR working plane that is head-relative, where the plane is attached to the head of the user as they move around the world. When the user moves through the world, the plane will be translated and rotated to remain fixed within the field of view. The main use for head-relative coordinate systems is the placement of display status information and object manipulation. Head-relative mode is the most natural choice for object movement since it allows the user to adjust all three degrees of freedom by moving the body.
|
Translate |
Head Rotate |
Translate / Head Rotate |
|
|
|
|
1.4 Plane creation
In order to take advantage of AR working planes, the plane must first be created in the environment. During creation, AR working planes must be located in one of the coordinate systems defined earlier, which will affect the operations that can be performed. This section discusses different methods of creating planes that may then be used for manipulation and vertex creation.
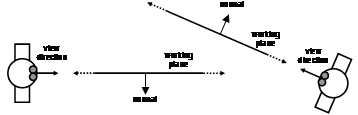
1.4.1 Created along head direction
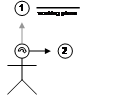
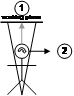
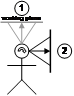
Figure 3‑9 depicts a user creating a plane originating from the userís head, parallel to the direction that the head is viewing. If the user is viewing in the direction of true north, then the plane will be infinite in the north and south directions, with east and west divided by the plane. Constraints may be applied to the orientation of the head so that only some degrees of freedom are used to create the plane. Since AR working planes are only useful when facing the user for cursors to be projected onto it, the user must be able to move independently of the plane to new viewing locations. This method is only relevant with world-relative coordinates since the plane is decoupled from the userís motion.
|
|
|
Figure 2‑9 AR working plane created along the head viewing direction of the user
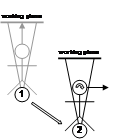
Figure 2‑10 AR working plane created at a fixed offset and with surface normal matching the view direction of the user |
1.4.2 Created at offset with user head direction as normal
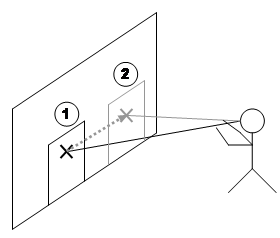
Figure 3‑10 depicts a user creating a plane that is located at a fixed distance away and with surface normal matching the userís view direction. If the user is viewing in the direction of true north, the plane will have a surface normal pointing north and be infinite in the east and west directions. Constraints may be used to restrict the degrees of freedom of the orientation of the head for creating the plane. Since the plane is facing the user it is ready to draw on and is suitable for use with all coordinate systems defined previously. The limitation of these planes is that the distance from the user must be specified with another input method, and the user may not be able to perform this accurately.
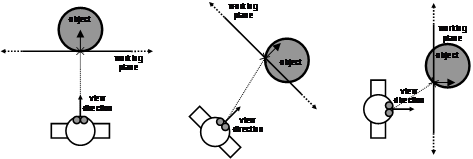
1.4.3 Created at an object with user head direction as normal
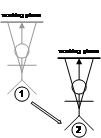
This technique is very similar to the previous in that the planeís surface normal is based on the userís view direction. The difference is that the plane is created so that it passes through the intersection point a user has selected on an object in the world. Figure 3‑11 depicts a user creating a plane at the intersection point of an object. These planes are most useful when created in head-relative coordinates for manipulation operations, although any other coordinate system is also possible.
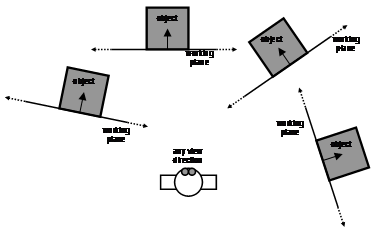
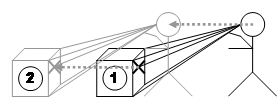
1.4.4 Created aligned to an objectís surface normal
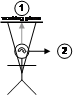
Figure 3‑12 depicts a plane created to match the surface of a nominated facet on an object. Each of the objects has an AR working plane that is coincident with the selected facet, making it invariant to the userís current position and orientation. As long as the object facet is visible and can be selected, then it can be used to spawn an AR working plane in the environment. Since the plane is created visible to the user it is immediately ready to draw on and is suitable for use with all coordinate systems. World coordinates are the most logical usage however, since the planes are defined relative to an object that is typically in world coordinates. Uses for other coordinate systems are discussed in the next sections.
|
|
|
Figure 2‑11 AR working plane created at intersection of cursor with object, and normal matching the userís view direction
Figure 2‑12 AR working plane created relative to an objectís surface |
1.4.5 Created at an intersection point using another objectís surface normal
Using a similar technique to that discussed previously, the facet of an object may supply a surface normal for an AR working plane created at another object. Figure 3‑13 depicts a plane created at the point where the userís cursor projection intersects an object in the environment. The surface normal is copied from an object selected previously with the same method. This technique is useful for manipulating objects relative to the surfaces of others and so is the most logical with world-relative coordinates, although other coordinate systems are possible as well.
|
|
|
Figure 2‑13 AR working plane created at a nominated object based on the surface normal of another reference object
|
|
|
|
|
|
|
1.5 Object manipulation
|
|
|
Figure 2‑17 Scaling of an object along an AR working plane with origin and two points
Figure 2‑18 Rotation of an object along AR working plane with origin and two points |
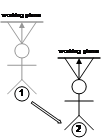
Given the ability to place down AR working planes in the environment, one possible use is the implementation of translate, scale, and rotate operations. The first step is to create a working plane in the environment using one of the previously described techniques relative to an appropriate coordinate system. The choice of coordinate system determines the type of operations that can be performed. When using AR working planes in head coordinates, these techniques share similar properties to selection using image plane [PIER97].
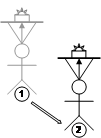
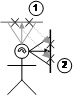
Translation operations where the object is accurately moved across the AR working plane surface can be performed as shown in Figure 3‑14. Two points are projected onto the plane and are used to calculate a translation. This translation is then applied to the object to move it to the desired location, with the offset always being along the surface of the plane. If the AR working plane is attached to the location, body, or head then varying the userís position will drag the object around, as depicted in Figure 3‑15. When using body or head coordinates, translations and rotations can be combined together, such as depicted in Figure 3‑16. By combining these techniques with cursor motion along an AR working plane, complex manipulation operations can be performed.
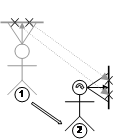
Scaling operations can be performed along the surface of an AR working plane and requires three input points Ė an origin for the scaling operation, and two points to specify a direction and magnitude vector. The two cursor points are used to calculate a new scaling transformation relative to the origin and then applied to the object, as depicted in Figure 3‑17.
|
|
|
Figure 2‑19 Vertices are created by projecting the 2D cursor against an AR working plane
|
|
|
|
|
Rotation operations can be performed about the surface normal of an AR working plane with three input points Ė an origin for the axis of rotation, and two points to specify an angle. The two cursor points are used to calculate a new rotation transformation relative to the axis of rotation and then applied to the object, as depicted in Figure 3‑18.
1.6 Vertex placement
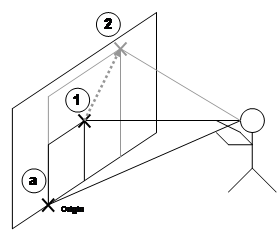
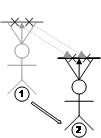
The second more novel use for AR working planes is the placement of points in the environment. Selection and manipulation of existing objects has been implemented previously using a number of techniques, but there is still a lack of techniques for the creation of new geometry at a distance. Figure 3‑19 depicts how a user can project the cursor against an AR working plane and create vertices anywhere on the surface. Similar to the previous object manipulation section, this operation can be performed using an AR working plane in any coordinate system and created using any technique.
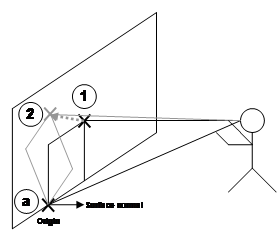
Apart from just creating points against fixed surfaces, if the AR working plane is relative to user coordinates then it will move with the motion of the user, as depicted in Figure 3‑20. As the user translates and rotates, the AR working plane will also move and points will be created in world coordinates against the current surface. While this technique may be used to create complex collections of vertices, this can be tedious for many objects. Chapter 4 will introduce techniques designed to simplify the creation of object geometry given certain assumptions.
1.7 Accurate alignment with objects
When creating AR working planes using the position and orientation of the body, it is important that the user be as accurately placed as possible. To create vertices specifying the outline of a building, working planes must be created that are in alignment with the walls. Any errors in the placement of the working planes will cause projected vertices to deviate from the true physical wall surface.
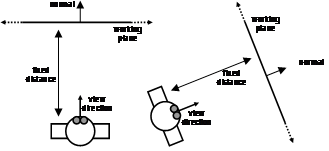
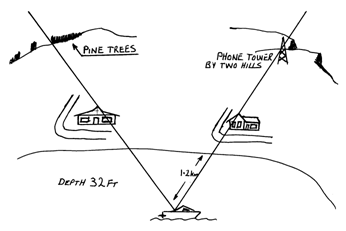
The eye is an incredibly accurate measuring device that can notice even minute shifts between two objects that are in alignment. While fishing offshore with my father, I was shown how to look at large features along the coastline such as hills, towers, and buildings. When a fishing spot was discovered that we would like to come back to, my father would look along the shore to find landmarks that were visually aligned. After selecting aligned landmarks, these would then be recorded in his diary, producing a diagram similar to the example in Figure 3‑21. Lining up two landmarks would place the boat along a particular bearing, and then lining up a further two landmarks along another bearing would fix the position of the boat down to the intersection of the two lines. We could accurately find previous fishing spots within a few metres accuracy without the use of any tools except visual inspection using the eye. Even when using his GPS unit, my father would only use it to get within its 5-10 metre accuracy and then use line of sight techniques to improve the position of the boat. The alignment of landmarks varies even when walking around the boat and so performing measurements from the same seating position is required to achieve the best accuracy. The main difficulty with this technique is that it is limited to spots where landmarks can be found to align. Books for amateurs by Pescatore and Ellis [PESC98] and the web site by Poczman [POCZ97] are examples of collections of fishing locations around Adelaide marked using this technique.
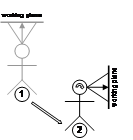
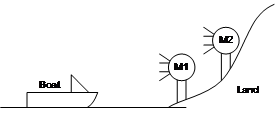
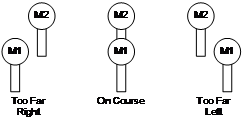
Bowditch describes similar techniques used by professional sailors when navigating close to shore [BOWD02]. Figure 3‑22 shows the placement of official navigational aids named range lights, which are used to indicate safe channels that boats can travel along. In many harbours there are obstacles that can easily damage ocean vessels, and so by keeping the range lights aligned the navigator can keep the ship very accurately in the marked channel without straying off course.
1.8 Alignment accuracy using HMDs
|
|
|
Figure 2‑21 Example fishing spot marked using various shore-based landmarks (Sketch courtesy of Spishek Piekarski)
Figure 2‑22 Example of range lights in use to indicate location-relative to a transit bearing (Adapted from Bowditch [BOWD02]) |
The alignment of landmarks can also be performed using a video-based HMD but with reduced accuracy compared to the eye since the resolution is much lower. According to Rose, the human eye has the capability to resolve single dots at approximately 1-2 minutes of arc [ROSE73], although the brain is capable of achieving resolutions at least one order of magnitude higher by processing the image further. In comparison, the HMD described in this section has a resolution of approximately 2 minutes of arc with no further enhancements possible. This section uses the easily measurable properties of a HMD to simplify the calculations, as the human vision system contains a wide range of processing that is not fully understood and difficult to model.
|
|
This section uses geometry to prove that the alignment of landmarks is useable with a video overlay mobile AR system to assist with the specification of planes in the environment. With landmark alignment, the creation of planes is limited mainly by the tracking equipment and not by the userís perceptive capabilities. Using the known parameters of a HMD and using the distance to two marker objects from the user, the maximum sideways translation the user can move without observing a change in alignment can be modelled. To simplify the calculations, subtle visibility effects that occur at sub-pixel levels when two objects appear to visually interact with each other will be ignored.
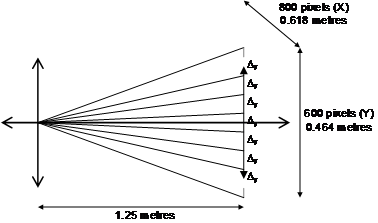
Figure 3‑23 depicts the layout for a Sony Glasstron PLM-700E HMD, which has a resolution of 800x600 pixels projected onto a focal plane 1.25 metres from the userís eye. The perceived image has approximate measured dimensions of 0.618 metres by 0.464 metres at the focal plane. Given this layout information, the size of each pixel may be calculated using similar triangles. Each pixel is approximately square and so is 0.773 millimetres in width and height at 1.25 metres. At a normalised focal distance of 1 metre, the pixels are 0.618 millimetres in width and height. Since each pixel is assumed to be square, normalised horizontal and vertical sizes are both represented using D.
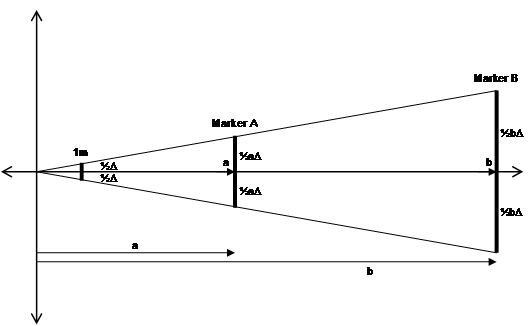
If a landmark at some distance is to be visible on the HMD, it must be projected onto at least one pixel (or a significant portion of a pixel) on the display. Given the previous distance of 0.618 mm for a pixel at one metre, this can be extended out for any distance with similar triangles. For example a 100 metre distant marker must be 61.8 mm wide to be visible as a single pixel on the HMD. Using this concept, a diagram of similar triangles can be drawn (see Figure 3‑24) with a marker A of width aD at distance a, and marker B of width bD at distance b. The minimum required size of these markers is proportional to the distance from the HMD.
|
|
|
|
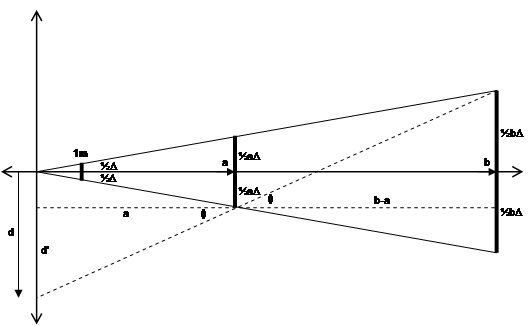
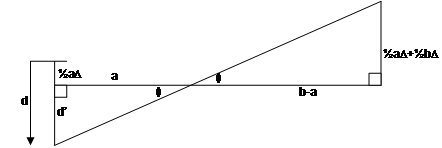
When the user and both markers are in line, there will be an exact overlap between the markers, and when viewed separately, each will form an image on the HMD that is exactly the same size. If the user moves sideways any distance at all, the objects will no longer overlap (as in Figure 3‑22) and appear to gradually separate apart. The goal of the following calculations is to estimate d from Figure 3‑25, the distance the user must move so that the projections of both markers no longer overlap (with a small gap between), ensuring visibility on the HMD. The distance d also represents the error in positioning possible using line of sight techniques, and can help to analyse their usefulness. The diagonal dotted line in Figure 3‑25 depicts the line that the user must look along to notice a separate pixel for each marker. To simplify the calculations, I assume that the markers appear on the display small enough that the geometry can be treated as straight lines rather than arcs. This is possible given the small size of the pixels in millimetres and the large distance of the markers in metres. Based on the dotted lines from Figure 3‑25, Figure 3‑26 depicts the arrangement of the similar triangles that need to be solved to estimate the error distance.
|
|
|
|
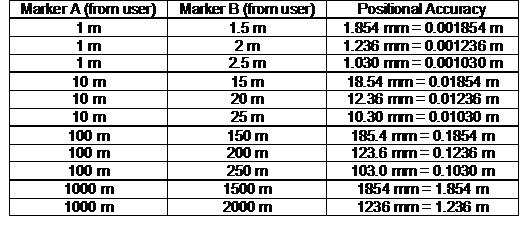
Using the similar triangles in Figure 3‑26, the equations can be derived to calculate a final equation that represents the accuracy d of this technique, shown in Figure 3‑27. This final error equation is useful because it allows a simple analysis of the accuracy of landmark alignment over a variety of distances. A single constant is used to linearly scale the equation depending on the pixel size calculated earlier. As the markers both approach the same distance, the technique rapidly increases errors due to an asymptote in the function when a=b. However, when the markers are sufficiently spaced apart from each other, the accuracy of the technique is quite incredible considering the distances involved. Table 3‑1 demonstrates this with the accuracies achieved using markers placed at different distances from the user.
|
|
|
|
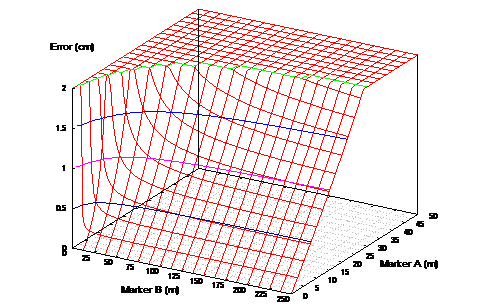
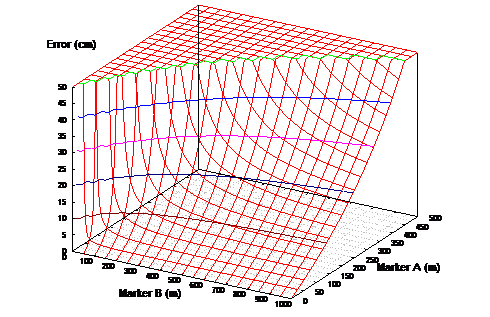
When working in a 3D environment, the tracking hardware will also impose limitations on the measuring accuracy of the system. If the landmark alignment is more accurate than that of the tracking hardware, it will be adequate for the required modelling task. Figure 3‑29 depicts a 3D surface with contour lines for the accuracy equation and is capped at the 2 cm limit of a Real-Time Kinematic GPS unit. Figure 3‑30 depicts a similar 3D surface restricted to the 50 cm accuracy obtainable from a high quality differential GPS unit. The sloped regions indicate distances where the accuracy of the technique is within the performance of the respective GPS units. As an example, using a building with corners at 100 metres and at 150 metres, this gives an accuracy of 18.54 centimetres that is within the accuracy of a 50 cm high quality GPS unit. This accuracy is quite poor compared to the 2 cm accuracy of an RTK GPS unit however, and to achieve accuracies better than 2 cm the near corner must be closer than 22 metres (therefore the far marker must be closer than 72 metres). These values may be calculated using the equation in Figure 3‑27.
|
|
Another property of landmark alignment is that as one landmark approaches an infinite distance, the slope of the 3D surface begins to match a linear approximation, most visible in Figure 3‑30. This slope is then only controlled by the distance of the closer marker, and as it moves toward the user the technique becomes more accurate. This property is useful when working with very long buildings at a close distance for example, where the further marker is so distant that only the close marker affects the accuracy of the technique. The equation in Figure 3‑27 can be rewritten into Figure 3‑28 to calculate the error in this case by using a limit with marker B approaching an infinite distance.
The previously discussed equations and graphs show that by visually aligning landmarks through a HMD, very accurate positioning of the body can be obtained. While a humanís ability to perceive depth rapidly attenuates as distance increases, the landmark alignment process is highly accurate over any distance given visible markers at a suitable distance apart.
1.9 Summary
|
|
Existing techniques for VR have been developed mainly to solve the problem of manipulating existing virtual objects at a distance, and do not address the problem of creating new vertices and geometry that are out of armís reach. This chapter demonstrated that a humanís ability to perceive depth rapidly attenuates in the vista space beyond 30 metres, making it difficult to correctly specify distances. Accurate depth specification is required to perform the modelling of large outdoor structures and these are almost always within vista space, and so suitable techniques are required to overcome the limitations of humans. I developed the concept of augmented reality working planes based on previously developed CAD and VR systems, performing the projection of 2D cursors onto 3D surfaces to specify depth information. AR working planes restricts degrees of freedom that the user is not capable of specifying accurately, and breaks the operation into logical tasks that can be easily understood by the user. AR working planes can be created using a number of methods, stored relative to world, location, body, and head coordinates, and used for object manipulation and vertex placement. By implementing working planes in AR, I take advantage of features that are only possible with the physical presence of the user in the environment. By using accurate positioning based on the alignment of objects in the environment, operations can be performed at large distances with only minor accuracy degradation caused by the user. AR working planes is a core concept for outdoor modelling used to support action at a distance, and the construction at a distance concept introduced in the next chapter.